Continuing to Contemplate Galilean Moon Motion

I decided to see if there are any explanations for what the higher-order derivatives (3rd, 4th, 5th) of position actually feels like, and I didn't get much of an answer.  However, they all have names.  The best source of info on this subject that I was able to find is this article:

What is Derivatives Of Displacement?

So yes, the 3rd derivative is called 'Jerk', which I call 'Bump' -- it's a change in acceleration.  The 4th derivative is 'Jounce' (the change in the 'Jerk') and 5th derivative is called 'Crackle' (the change in the 'Jounce'), which to me don't relay any kind of physical sensation.

In the case of the motions of Jupiter's Galilean moons, I can now look at the past seven days of motion:

Galilean Moon Motion 08 June 2017

Looking at the motions of the four Galilean moons of Jupiter.  The following plots are for 08 June 2017.

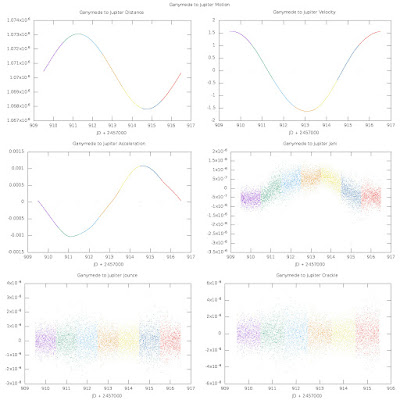
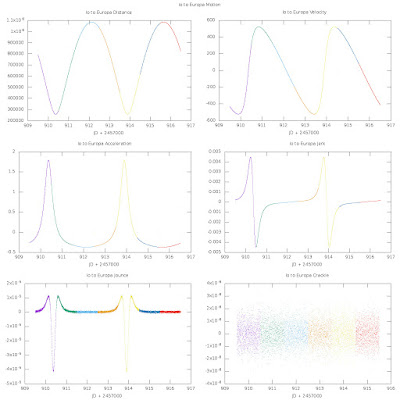
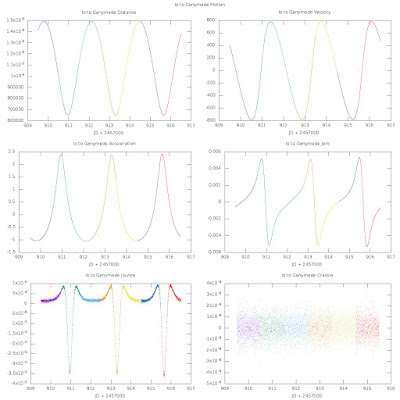
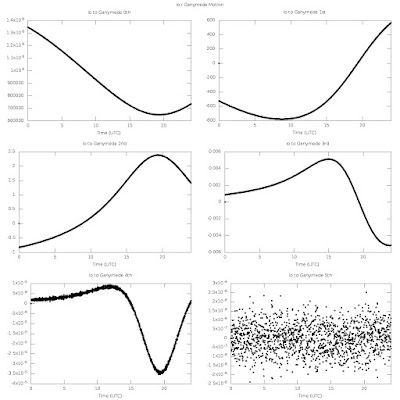
In all of these plots, I'm showing the 0th (position), 1st (velocity), 2nd (acceleration), 3rd, 4th, and 5th derivatives of position as a function of time.  So the 0th derivative is in km, 1st is km/minute, 2nd is km/min^2, 3rd is km/min^3, 4th is km/min^4, and 5th is km/min^5.  What do the higher-order derivatives feel like?  Not sure, but the 3rd order probably feels like a bump (a change in acceleration).


Io motion around Jupiter:

Europa motion around Jupiter:

Ganymede motion around Jupiter:

Callisto motion around Jupiter:

Io motion relative to Europa:

Io motion relative to Ganymede:

Here's how the 4th derivative sounds:


Io motion relative to Callisto:

Europa motion relative to Ganymede:

Europa motion relative to Callisto:

Ganymede motion relative to Callisto:

All of this will be converted to audio so I can experience how it sounds.

Chaos Plots

These images are based on the equation:

N+1 = (lam) * N * (1-N)

where 'N' is the current population level (scaled between zero and one) and 'N+1' is the next population level.  'lam' goes from zero to about five until things get a bit crazy.

This little work is based on the video:

https://www.youtube.com/watch?v=ETrYE4MdoLQ

In the plots below, the x-axis is the 'lam' value, and the y-axis is the 'N' value.